What is a Filter Bank?

Consider an input audio signal $x(n)$. This signal might have come from a microphone, or the pickup on an electric guitar. To learn more about the sampling process used to obtain $x(n)$, consult the digital waveguide model laboratory assignment.

As discussed briefly in the monochord laboratory assignment, the spectrum of a signal gives the distribution of signal energy as a function of frequency. One commonplace situation where the concept of a spectrum arises involves the tunable equalizers found on many home and car stereo systems. In their simplest form, these equalizers may consist of two controls to adjust the level of bass and treble in the audio signal played through the system speakers. The bass control allows the user to adjust the level of the lower-frequency energy in the signal spectrum, whereas the treble control allows for the adjustment of higher frequency energy in the spectrum. Other equalizers are more advanced; many often have several controls to adjust the strength of various separate regions in the signal spectrum. In all cases, however, it is necessary to think of signal energy as a function of frequency, as provided by the spectrum concept.

In order to separate energy from a frequency region of a signal's spectrum, a bandpass filter may be used. An ideal bandpass filter rejects all input signal energy outside of a desired frequency range, while giving as output all input signal energy within that range. The range of accepted frequencies is often referred to as the band, or passband. The frequency boundaries defining the band, $f_{\mathrm{cl}}$ and $f_{\mathrm{ch}}$, are known as the lower and upper cutoff frequencies (respectively). These are also referred to as the band edges. The difference between the upper and lower cutoff frequencies is known as the bandwidth:

$$BW = f_{ch} - f_{cl}.$$ (1)

The midpoint of the band edges is known as the center frequency $f_c$ of the bandpass filter. Finally, the ratio of the center frequency $f_c$ to the bandwidth $BW$ of the filter is called the quality factor:

$$Q = \frac{f_c}{BW}$$ (2)

A sketch showing the frequency response of an ideal bandpass filter with key features labeled is shown in Figure 1.

Figure 1: Sketch of the frequency response of an ideal bandpass filter, with key features labeled.

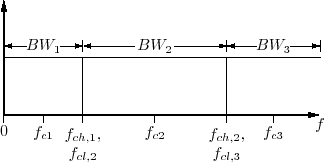
A filter bank is a system that divides the input signal $x(n)$ into a set of analysis signals $x_1(n), x_2(n), \ldots$, each of which corresponds to a different region in the spectrum of $x(n)$. Typically, the regions in the spectrum given by the analysis signals collectively span the entire audible range of human hearing, from approximately 20 Hz to 20 kHz. Also, the regions usually do not overlap, but are lined up one after the other, with edges, touching, as shown in Figure 2. The analysis signals $x_1(n), x_2(n), \ldots$ may be obtained using a collection of bandpass filters with bandwidths $BW_1, BW_2, \ldots$ and center frequencies $f_{c1}, f_{c2}, \ldots$ (respectively).

Figure 2: Sketch showing the bands of a three-band filter bank, with adjacent band edges touching but not overlapping. Together, the 3 bands span the frequency range from $f_{cl,1} = 0$ Hz to $f_{ch,3} = f_\mathrm{max},$ where $f_\mathrm{max}$ is the maximum frequency of interest (not shown).