Next |
Prev |
Up |
Top
|
REALSIMPLE Top
Third-octave filter banks have historically been popular in audio analysis, as
the bandwidths of these types of banks have been shown to loosely approximate
the measured bandwidths of the auditory filters. Third-octave banks have also
been internationally standardized for use in audio analysis [1].
In a third-octave filter bank, the center frequencies of the various bands
![$f_c[k]$](img18.png) are defined relative to a bandpass filter centered at
are defined relative to a bandpass filter centered at ![$f_c[0] = 1000$](img19.png) Hz, by the following formula:
Hz, by the following formula:
![\begin{displaymath}
f_c[k] = 2^{k/3} 1000 \mathrm{Hz.}
\end{displaymath}](img20.png) |
(3) |
The upper and lower band edges in the 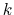 th band are further given by the
geometric means
th band are further given by the
geometric means
![\begin{displaymath}
f_{ch}[k] = \sqrt{ f_c[k] f_c[k+1] },
\end{displaymath}](img22.png) |
(4) |
and
![\begin{displaymath}
f_{cl}[k] = \sqrt{ f_c[k-1] f_c[k] },
\end{displaymath}](img23.png) |
(5) |
respectively. From the above equations, it may be shown that the bandwidth of
the 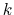 th band is given by
th band is given by
![\begin{displaymath}
BW[k] = f_c[k] \frac{2^{1/3} - 1}{2^{1/6}}.
\end{displaymath}](img24.png) |
(6) |
It may be shown that as the bandwidth in Equation (6) above is proportional to
center frequency, the quality factor of each third-octave band filter is
independent of 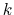 . As a result, filter banks such as the third-octave bank
are referred to as constant-Q filter banks.
. As a result, filter banks such as the third-octave bank
are referred to as constant-Q filter banks.
Next |
Prev |
Up |
Top
|
REALSIMPLE Top
Download aud_fb.pdf
![]() are defined relative to a bandpass filter centered at
are defined relative to a bandpass filter centered at ![]() Hz, by the following formula:
Hz, by the following formula: