This chapter presents nineteen tutorials on signal processing objects. These descriptions correspond to patches with the same numbers in the doc/tutorials directory of the Ircam Max/Fts distribution.
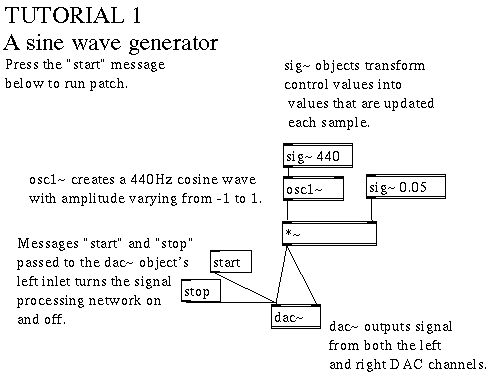
This patch uses an oscillator object to generate a cosine wave with a constant frequency of 440 Hz. We then scale the cosine's amplitude to a reasonable listening level and play it from both the left and right output channels.
While most patches contain a mix of signal processing and control objects, one must keep in mind the differences between the two types, and to treat them accordingly.
Now use the File menu in Max to open 01sine_tut.pat

To run the patch: click on the message box start. To turn off the patch, click on stop.
The heart of this cosine wave generator is the osc1~ object. osc1~, with no arguments, takes frequencies at its left inlet, an optional phase value at its right inlet, and generates a cosine wave varying in amplitude between +1 and -1.
In order to function, osc1~ needs to know at all times the frequency of the cosine wave it is to create. To provide this continuous frequency information, we use a sig~ object. sig~ is the simplest tool for converting control messages to signals: any discrete value input to the object (either passed to the inlet or typed as an argument) is output continuously from the sig~'s outlet until a new input message is received. In this patch, for example, sig~ 440 generates a continuous stream of 440s.
The same principles apply as we scale the amplitude of the oscillator's output. Since the range of +1 to -1 is too loud to tolerate (this represents a maximum amplitude), we multiply the cosine wave by a constant of .05 (or 1/20th of the original maximum amplitude). To do this, we use the signal multiplier *~. This object, like osc1~ and many other signal processing objects requires signals, and not control messages, at its inlets. We are obliged, then, to use sig~ to turn .05 into a continuous stream of .05s that the multiplier object accepts.
We now have an amplitude-scaled 440 Hz sine wave coming from the outlet of the *~ object. In order to hear the sound, we send the signal to the digital to analog converters (DACs). In Max, the DACs are accessed using the object dac~ whose two inlets take signals intended for the left and right output channels. In addition, the left inlet takes two important control messages: start and stop. (We will see later that many signal objects also take control messages that change the "state" of the object+/-or modify their behavior in some way).
The start and stop messages do more, in fact, than control the DACs, they turn the Max signal processing network on and off. Unlike the control objects in Max, which are "active" as soon as they are instantiated, the signal processing objects must be explicitly turned on before they begin calculating. There can be many dac~ (and corresponding adc~) objects in a patch even if, physically, there is only one DAC device connected to the card; signals to multiple dac~ objects are added together before being output. Sending any dac~ object a start or stop message affects the entire currently open signal processing network. Lastly, changes in the signal processing part of a patch will not go into effect until a new start message is sent.
This patch improves the cosine wave generator from Tutorial 01 with the following features:
line~ takes a target value at its left inlet and a time (in ms) at its right inlet. Usually the two messages are specified as a list target time at the left inlet. When a new message appears at the object's left inlet, line~ creates a continuous line segment, or interpolation, between its current value and the new target value, taking the amount of time specified at the right inlet to complete its trajectory. Like sig~, line~ converts control messages to signals. Thus, while its input takes discrete messages like "go to the value 4 in 3 seconds," expressed as "4 3000," the output of the object is continous.
Let us examine the behavior of the line~ object in this patch. When the dac~ object receives the start message, line~ begins to output zero, once each sample. As soon as the message sent to amp is received (0.1 1000) the output from line~ gradually increases from 0, which is the current state, to 0.1, the new target. In exactly one second, line~'s output will have reached 0.1. This 0.1 will continue to output from line~ once each sample, until a new message is received at the left inlet. If, for example, we click on the message box marked "Off", the line~ object would receive the message 0 500, and thus its output would start decreasing from its current state: 0.1, to its new target: zero. After a half second (500 ms), the output reaches zero, and stays there until a new message is received.
This simple breakpoint envelope generator might be useful in a number of situations. In this example, we multiply the sine wave output from osc1~ by the output of line~ to control output amplitude continuously.
In this patch, the frequency of the sine wave is no longer fixed at 440 Hz as it was in the first tutorial; instead, frequencies are determined by incoming MIDI notes. The object notein provides MIDI input to the patch, reporting note numbers from its left outlet and corresponding velocities from its right. The object stripnote takes away note off messages (i.e., notes with velocities of zero) which are not necessary for our purposes. For the time being, in fact, we ignore velocity information altogether, connecting only the MIDI note number outlet of stripnote. These MIDI values are then converted into frequencies (in Hz) by the object mtof, and sent using a send object labeled freq. Messages recieved by the corresponding receive object are subsequently converted to a signal using sig~. Finally, the result is used to control the frequency of the oscillator.
Tutorial III uses osc1~ in conjunction with tab1~ to generate triangle and square waves. It also uses phasor~ to create a sawtooth wave.
As we have seen, osc1~ used alone and with no arguments outputs a cosine wave. osc1~ can also be used to read through a user-defined wave form which is loaded and stored by the tab1~ object.
When a patch containing a tab1~ object is opened, tab1~ reads in the short NeXT soundfile whose pathname is given as the argument for the object. tab1~ removes the header information from the soundfile, converts the first 512 samples into floating point numbers between -1 and +1, and stores the result in memory. This being done, all osc1~ objects in the patch with the same pathname refer to those memorized samples, cycling through them to make a periodic wave form.
In our example, two different waveforms are imported using the tab1~/osc1~ combination. For the sawtooth wave, which is often useful as a control signal, the object phasor~ is used. phasor~ is a sawtooth wave generator that takes a signal at its input to determine frequency (in one period, the sawtooth wave makes a continuous ramp from zero to one). Like the osc1~ object, the phasor~ object can take a floating point message between 0 and 1 (corresponding to 0° to 360°), to reset its phase.
The patch realizes a simple phase modulation tone generator using two cosine wave oscillators.
One relatively easy way to create rich and complex timbres is to modulate a sine wave's phase with another sine wave whose frequency is in the audible spectrum.
To understand what it means to phase modulate a waveform in Max, imagine an oscillator as having a pointer, or phase index that cycles repeatedly through a single memorized sine wave period.
For convenience, think of the course of the oscillator's phase index as being circular. We will speak of the reader's location on its circular path at any given time in terms of an angle, which in fact, is the phase of the waveform.
If the phase index follows its normally around the circle at the rate of one revolution per period, the oscillator outputs an normal unaltered sine wave. If, however, we force a different course upon the reader, we will get out a different, complex waveform. John Chowning showed that using one sine wave to control another's phase in this way can lead to interesting and predictable results. This patch implements the idea by passing the ouput of one osc1~ object into the phase (right) inlet of another. Values between 0 and 1 to this input correspond to 0° to 360° values greater than 1 wrap around (i.e., 12.53 will be taken as .53).
Note that the patch consists of two nearly identical parts. In fact, the only difference, other than frequency, between the two cosine generators are their comment labels; this is done to reflect their different roles. The oscillator which does the modulating is called the modulator, and the one which is modulated is called the carrier. The control of the amplitude of the modulator is called modulation depth, or index. This last parameter controls the magnitude of variation introduced to the carrier's course.
This patch uses multiple copies of the phase modulation tone generator from the preceding patch to make a simple eight voice polyphonic synthesizer.
To examine all the elements of this patch, double-click on the patcher FMvoice, and then on the subpatch FMengine.
The FMengine patch is an abstracted version of the phase modulation sound generator from the previous tutorial, the only difference being that incoming MIDI controller values are divided by127 to convert them into an "index" between 0 and 1. In the layer above, the patcher FMvoice, messages which control sound parameters are sorted and sent to the FMengine module. Pitches to be played come into the FMvoice module as lists of MIDI notes and their corresponding velocities (we will see, momentarily, how they got there).
After unpacking the note - velocity lists in order to separate them, we convert the MIDI notes to frequencies using the mtof object. Each newly converted pitch is entered as the carrier frequency, and divided by a constant (3.7) to provide the modulator frequency. The modulation index is initially set to 50 (remember that 0 - 127 is scaled to a number between 0 and 1 inside FMengine). Later we will change the modulation index using a MIDI controller. MIDI velocity information is scaled down and multiplied with the output of FMengine. This provides velocity control (including note offs) for each module.
We have made eight copies of this FM module in order to have up to 8 voices at a time. The poly object allocates incoming notes among them. poly takes incoming <note velocity> lists and outputs them along with a voice number. It keeps track of which voices are currently playing, makes sure that note offs are sent to the right voices, and turns off the old voices to make room for new ones ("voice stealing"). Its two arguments are number of voices and voice stealing on/off (the presence of a second argument turns voice stealing on). To allocate incoming pitches to FMvoice subpatchers, we pack the output of poly into a list and send the result through a route object. The first number of the list, a voice number calculated by poly, will be interpreted by route as the outlet to which it should send the rest of the list <note velocity>. To these outlets we connect the FMvoice modules.
Finally, to add the outgoing signals of all the FM modules we use the throw~ and catch~ objects. catch~ outputs the sum of all throw~ objects which share its name. Their are usually multiple throw~ objects with a given name, whereas there can only be one catch~.
It is extremely useful to organize large patches into smaller units called subpatches. This is especially true when a patch contains several copies of a given interconnected group of elements. Information passes in and out of subpatches via inlets and outlets.
There are two ways to create subpatches: recalling saved patches and the patcher object. Any patch that you have made can become a subpatch. Simply type the name of an existing patch into an object box (if it is in a different directory than the patch which calls it, specify the full path name), and the module becomes an abstraction of that patch.
Warning: If you edit a subpatch, its source is edited as well.
The second method, the patcher object, creates subpatches that are local to the patch in which they live. Hence a subpatch of patch "foo" is not accessible to patch "bar" (one can, of course, always copy and paste). Furthermore, multiple instances of a subpatch in a given patch are independent--meaning that editing a single copy does not effect the others.
Different situations call for their own versions of a subpatch. For example, in this tutorial, "FMengine" is a subpatch of the first type. This is because it is a basic unit which is more or less flexible and which might be useful in many different applications. The subpatch FMvoice, on the other hand, is of the second type because it makes a few arbitrary decisions which are "hard-wired" (like the mod frequency being defined as half of the carrier), and is thus probably only useful in this example patch. Additionally, the user might want to vary the different instances of FMvoice (to have slighlty different mod frequency ratios, for example).
This patch implements a simple delay of a signal input to the ADCs.
To understand how delays work in Max, imagine them as pipes into which signals are funneled. It takes time for a signal to make its way from one end of the pipe to the other. If we sing into a 340-meter pipe that takes one second for sound to traverse, and listen to the far end, we hear our voice one second later. delwrite~ creates a pipe, gives it a name (its first argument), and a length (its second argument), expressed as the time it takes to go from one end to the other.
To listen to the delay, we can drill a hole, or tap, anywhere along the length of the pipe. This permits us to have a delay of any period we want, provided that it's less than the total length of the delay line. Furthermore, we can have several taps in different places along the delay line. One way to make a tap is with the delread~ object. (vd~ can also tap a delay line. We will see this in the next tutorial.) delread~ takes the name of the delay line to tap and the position of the tap in milliseconds as arguments .
In this patch, then, we start with a signal coming in from the ADCs using the object adc~. The two outlets of the adc~ object output the left and right input channel signals. In this case, as the author does not know to which channel the mono microphone (or other sound source) is connected, we add the two channels together using a +~ object. This signal is then written into a delay line of 1500ms which we will name joe-del. (The name is arbitrary, we could have named it my-del or foo.) The delay line is then tapped, initially at 1 sec, with a delread~ object (now the name joe-del is important because it refers to a delay line created with delwrite~+/-there can be several different delay lines in a patch). The slider on the right hand side of the patch sends new messages to the delread~ object, changing the point at which the line is tapped and and hence the delay time. Change the slider's position to hear the difference in delay time.
This tutorial is virtually identical to the preceding one, with the important difference that the delay line is read with the object vd~ instead of delread~.
Unlike delread~ which takes a control message at its input to define a tap point, vd~ takes a signal input, updating the tap point continuously. The most obvious use of vd~ is in a patch where one must change the delay time (delread~ clicks if the time is changed).
Changing the tap point at the signal rate can also produce a very interesting side effect. Imagine that the tap point goes from 0 to the length of the delay line at exactly the same speed as the delayed signal. In fact, we would always be listening to the same sample! Imagine now that the tap is moving slightly slower than the signal. The signal would pass over it, but at a much slower rate than it would of if the tap had remained still; we have thus created a transposition with a delay line.
This patch realizes a more complicated delay system, with feedback and a different delay time for the right and left channels.
Two things distinguish this delay patch from Tutorial 06. One modification is the addition of a feedback loop. The general term "feedback" means that part of a processed signal is injected back into the processor along with the unprocessed signal, thus forming a loop from the output back to the input. We all know the unpleasant example of feedback that occurs when a microphone is too close to the loudspeaker that amplifies it. This kind of nasty "infinite" feedback loop can happen with our delay patch as well. For this reason, we scale the delayed signal by half before adding it to the incoming signal and writing it back into the delay line. In doing so, we create a repeating echo with an ever-decreasing amplitude.
The second addition to this patch is the alternation of echoes between the right and left channels. This also illustrates the possibility of making multiple taps into the same delay line. In this case, the right channel is always reading at half the time of the left channel. Because of the feedback loop, the delay line stays active long after we have stopped providing input from the ADCs, and at every 500 ms interval, one of the two channels outputs the signal.
This patcher implements a simple sampler that is capable of recording up to two 5 second mono sa
mples and playing them back at varying speeds.
Sampling in Max involves three objects:
This patch allocates memory for two samples, named my-sample1 and my-sample2. Each sample has a maximum length of five seconds. We enter the signal we wish to record (in this case, input from the ADCs) into the inlets of two sampwrite~ objects. To begin recording into one of the two sample tables, we send a bang to the corresponding sampwrite~ object's inlet. Five seconds after sending the bang, recording is finished and the sample is stored in memory+/-ready to be played.
To playback the sample, we must provide the sampread~ object with a signal input that acts as an index into the sample memory. The simplest way to make an index signal, if we wish to read the sample in a linear way, is to use the line~ object. For example, to read a five second sample at normal speed from beginning to end, we connect a line~ to sampread~, and send it the message "0, 5000 5000". This tells line~ to start at 0, and to output a continuous linear ramp to 5000 over the period of 5 seconds. To read the sample backwards at normal speed, we send line~ the message "5000, 0 5000", telling it to output a ramp starting at 5000 and going to 0 over the period of 5 seconds. To read the sample forward at faster than normal speed (thus transposing it as well), we send the message "0, 5000 4000", meaning start at 0 and go to 5000 (the end of the five second sample) in the period of 4 seconds. To start in the middle of the sample, we send the message "2000, 5000 3000", meaning start at 2 seconds and play the remaining 3 seconds in 3 seconds.
In the part of the patch labeled "scrub", we use a slider to read the sample. First we multiply the slider's output by 40 to scale its output, and then we pack the outgoing message into a list with 500 before sending it to line~. The value 500, which becomes line~'s time argument, smooths slider's ouput. A smaller time value causes the index value to jump so abruptly that sampread~ clicks or makes otherwise undesirable results.
The message set sample-name sent to sampread~, tells the object to refer to a different table~ object (sampwrite~ also takes the set sample-name message. Try recording two samples and switching between them during playback. You will see that the transition from one sample to another is quite smooth and seamless.)
This patch lets you record a two second soundfile to the hard disk, and to play it back through the DACs.
As opposed to samples, which are stored in the IRCAM Musical Workstation card's memory, soundfiles reside on the NeXT computer's hard disk. They therefore provide a more permanent and ample storage for recorded sounds. Manipulating soundfiles, however, is neither as rapid nor as flexible and manipulating samples in the card's memory.
Recording soundfiles with the writesf~ object is a three-step process:
The goal of this patch is to automate the process of soundfile recording and playback so that both can be triggered with a simple bang message.
threshold~ takes a signal as input, and emits a bang from its left outlet when the signal's amplitude increases to a threshold defined by the object's first argument (in this case 0.01). The second argument defines the minimum time between two triggers; here, triggers can come no more than once per second. The threshold~ object also takes an optional third and fourth argument which define a threshold for a signal decreasing in amplitude+/-this causes a bang to be sent from the right outlet+/-but we do not make use of this feature in this patch.
The threshold~ object thus monitors the incoming signal, and sends bang each time its amplitude exceeds 0.01. When the gate is open, the bang is passed along, triggering the message to start recording. The bang also sends a "0" to the gate to close it again, so that only one trigger can get through. Three seconds after recording begins, the message write_it 0 is sent and the recording is stopped.
One possible problem with this method is that in the time it takes the automation mechanism to react and start recording, the first few milliseconds of a sound have already passed. We correct for this by piping the incoming signal through a 50 millisecond delay line before sending it to writesf~. By doing this, the recorded signal is always 50 ms "older" than the one used to trigger recording.
This patch directs an incoming signal alternately through a reverberator and a delay using the switch~ object.
The switch~ object allows one to turn independent parts of a signal network on and off dynamically. In this tutorial, one source signal is passed through two independent processing modules, each controlled by its own switch~ (the modules are activated by sending the switch~ a "1" or "0").
In order to be controlled by switch~, all the signal objects in a given network must be unambiguously part of the same signal path. For example, if you open the patcher "delay", you will see that there are some connections which seem extraneous, like the connection between the inlet and the sig~ object. In fact, this is a "dummy" connection which does not pass information, but serves to link sig~ to the switch~ which controls it. When using switch~, this dummy connection is necessary; without it, the sig~ would always calculate, even if its output were going to objects which were correctly turned off.
Extracting result signals out of a switched network is a bit tricky. If, for example, we added the outputs of "patcher delay" and "patcher reverb" and sent the results to the DACs, we would have a serious problem because the +~ used to add the signals together would fall under the switch~ state of both. To avoid this problem, throw~ and catch~ are used extract a result signal from a switched network. As we saw in Signal Processing Tutorial 05, catch~ adds all the signals sent to throw~ objects which share its name (argument). The state of a switch~ does not traverse the throw~ catch~ connection.
This example illustrates a sample-and-hold algorithm: a wave (sawtooth) is periodically sampled using another sawtooth wave, and the result controls the frequency of a sine wave generator.
The key to this patch is the samphold~ object. samphold~ takes two signal inputs: a control signal at its left inlet, and a signal to be sampled at its right inlet. While the control decreases in amplitude, the sampled signal is passed directly to samphold~'s outlet. When the control signal increases in amplitude, the output of samphold~ is "held" at the last value of the sampled signal.
In our example, the control signal is a sawtooth wave which, by its definition, decreases in amplitude only once each period. Thus, for each period of the control signal, one new value is let by--or sampled--from the sawtooth wave at the right inlet and then held until the control signal's next period. Since the two sawtooth waves have different frequencies, this has the effect of sampling different points along the right inlet signal's course.
These values are then multiplied by 440, and the results are used as the frequency control for a cosine wave generator.
This patch demonstrates bandpass filtering a noise source.
The wahwah~ object is a bandpass filter whose parameters--center frequency and Q--can be changed dynamically without clicks. The filter parameters are given as signals and not as control messages. Here we use line~ objects in order to change values smoothly.
In this patch, we pass white noise alternately through a lowpass and highpass filter, providing controls for cutoff frequency and output amplitude.
The heart of the two filter subpatches in this tutorial is the 2p2z~ (two pole two zero) filter object. This object takes floating point filter coefficients as arguments and inputs, as well as the signal to be filtered.
Digital filter theory is beyond the scope of these tutorials, but if you are familiar with filters, the 2p2z~ works as follows:
If the input is x[n], the output is y[n], and letting z[n] be temporary, the filter is defined as:
z[n] = c0 * x[n] + c1 * z[n-1] * c2 * z[n-2];
y[n] = d0 * z[n] + d1 * z[n-1] +d2 * z[n-2].
For those who are familiar with the use of filters but not their construction, modify the subpatches in this tutorial to create custom lowpass and highpass filters. Note that these subpatches are dependent on the sample rate and thus must be altered to work at rates other than 44100 Hz.
This patch tracks the amplitude of an incoming signal and convertes it to dB.
The power of a signal is defined as the average of its square, so we start by multiplying the signal by itself and sending it through a lowpass filter. The lowpass filter averages the signal in time, smoothing out bumps and transients in the signal, thus reducing its high frequency content.
In order to display the signal's amplitude on the slider in terms of dB we must convert it from a signal to a sequence of control messages with the object snapshot~. snapshot~ takes a signal at its input and a bang message. Each time a bang is received, snapshot~ reports the amplitude of the current sample. Here, a metro object is used to send bangs to snapshot~ every 100 ms.
Values output from snapshot~ (amplitudes from 0 to 1) are then converted with the formula shown in the expr object so as to display in dB on a scale of 0 to 127. The scale marks next to the slider object were made by hand to reflect real dB values.
This patch tracks the pitch of a signal input to the ADCs and of a sinewave oscillator. Both discrete MIDI and continuous frequency are output.
Pitch tracking in Max is done with the pt~ object. pt~ takes a signal at its inlet along with a variety of control parameters, and outputs an estimate of the signal's perceived pitch. From the left outlet, a MIDI note number is output each time pt~ decides that a new pitch has occurred. From the right outlet, a frequency value is output each time pt~ is polled by a bang to its inlet. We provide several sets of example parameters for pt~ in the patch, the function of each parameter is given below:
amp[i] * coef[0] + amp[i + 24] * coef[1] +
amp[i + 38] * coef[2] + amp[i + 48] * coef[3] +
amp[i + 56] * coef[4] + amp[i + 62] * coef[5] +
amp[i + 67] * coef[6] + amp[i + 72] * coef[7].
power[i] + power[i + 24] + ... + power[i + 72]
______________________________________
total-signal-power-up-to-(i+72)
A note will not be detected unless a raw pitch is found and the turn-on quality is exceeded; a raw pitch won't even be reported unless the turn-off amplitude is exceeded. Thus, if the RMS ever goes below the turn-off amplitude and then increases to exceed the turn-on one, a new note will be output
This patch analyses an incoming signal using the fast Fourier transform (FFT), and displays the power spectrum for 16 frequency bands on 16 sliders.
The fft~ object takes three arguments: the number of sample points per FFT, the number of points between the beginnings of each successive FFT, and an offset value. The object outputs a series of amplitude values which correspond to the amount of energy at given frequency bands. The number and width of the bands (called frequency bins in the parlance of signal processing) depends on the number of points in the FFT. If there are 512 points, the audible spectrum will be divided into 512 equally sized frequency bins. These values are expressed in their separate real and imaginary parts, output from the left and middle outlets of the fft~ object respectively. To convert these values so that they represent the power spectrum of the signal, we take the sum of the squares of the real and imaginary parts. (To obtain the amplitude spectrum, we would take the square root of this result).
As the FFT's serial output is difficult to manage, we first write the data into a table~ called fft-sample. We trigger sample recording with a bang that the fft~ object sends from its right outlet between each successive FFT. At any given time, then, "fft-sample" contains a mix of information from the current FFT and the previous one. (Having some information which is one-FFT-old does not pose much of a problem for this application.)
To access the frequency bin information stored in "fft-sample", we use the samppeek~ object. samppeek~, when given a floating point time value at its inlet, indexes the table~ named in its creation argument, and outputs the sample value for that time. The 16 samppeek~ objects in this patch report frequency bins equally spaced at . 02 ms intervals. Values are given every 100 ms (the polling is staggered by a 50 ms offset to avoid executing 16 samppeek~s at exactly the same moment).
In this patch, we construct a simple Karplus-Strong plucked-string synthesizer that can be controlled via MIDI.
In the Karplus-Strong algorithm, a random signal (noise burst) is injected into a short delay line with feedback. On each feedback iteration, the signal is sent through a lowpass filter which averages adjacent samples. Using a lowpass filter in this way creates an exponential decay in the sound wherein high frequencies die out more quickly than low ones. The result is a realistic plucked string simulation.
The pitch of the sound is determined by the length of the delay line. In order to have our desired pitch expressed as a period in milliseconds, we divide 1000 (ms) by incoming frequencies (converted from MIDI notes). For each note, we make this calculation, send the result to the delread~ object, and then send a bang to a trigger which fills the delay line with a noise burst. The noise burst then circulates through the feedback loop, passing each time through a 2p2z~ filter object that averages adjacent samples. The result from the filter is then multiplied by 0.99 in order to accelerate the decay.
A current limitation of Max is that it can not handle feedback delays of less than 64 samples. For this reason, it is impossible to create notes higher than about middle C using this patch.
This patch realizes a flange effect by adding a signal to a variably delayed copy of itself.
The variable delay loop that creates the flange effect can be seen on the right side of the patch. Here, the output of an osc1~ object is scaled to produce a cosine wave with amplitude values between 10 and 30, and these values are used to control the delay time of a vd~ object. The delay line is filled with the sum of the unprocessed input signal and the delayed signal. The amount of delayed signal added to the original and written back into the feedback loop is determined by the value, "flange-loop".
The value flange-amp also controls the amount of delayed signal added to the original. The result of this calculation is sent to the DACs (by way of a lowpass filter) and not written back into the delay line.