• General Wave Properties
• Superposition
• N-Mass Systems vs. Distributed Systems
• The Wave Equation (for a stretched string)
• Traveling Waves
• Wave Reflection
• Refraction
• Diffraction
• The Doppler Effect
• Sound Waves

Wave Phenomena

Wave motion involves the transfer of energy. The behavior of this energy transfer varies with the particular medium of transport and energy form. Mechanical waves travel in a material medium, such as water or a string.

General Wave Properties

• Wave motion is initiated by a disturbance which subsequently travels through a medium with a fixed velocity (for homogeneous media).

• A disturbance is transported through a medium via internal cohesive forces, though the medium itself is not transported.

• A simple sinusoidal disturbance of frequency 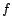$f$ will produce periodic motion with a wavelength given by 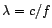$\lambda = c / f$, where 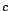$c$ is the wave speed of propagation.

• The wave speed is determined by the mass (or mass density) and elastic modulus (or tension) of the medium in which it travels.

• Longitudinal Wave Motion: vibration of particles in the medium is along the same direction as the wave motion.

• Transverse Wave Motion: vibration of particles in the medium is perpendicular to the direction of wave motion.

Superposition

• When two or more waves pass through the same region of space at the same time, the actual displacement is the vector (or algebraic) sum of the individual displacements.

• By Fourier's theorem, any complex wave can be considered as composed of many simple sinusoidal waves of different amplitudes, wavelengths, and frequencies (Matlab example).

N-Mass Systems vs. Distributed Systems

• An N-mass system has N modes per degree of freedom.

• As N gets very large, it becomes convenient to view the system as a continuous string with a uniform mass density and tension.

The Wave Equation (for a stretched string)

• ``Equation of motion for a wave''.

  Figure 10: Short string section.

  

• The mass of the short string section (length $\Delta x$) is $\mu \Delta x$, where $\mu$ is the mass per unit length of the string.
• The net vertical force on the section is $T \sin \theta_{2} - T \sin \theta_{1}$.
• For small angles, $\sin \theta \approx \tan \theta$ and $\tan \theta = \frac{\partial y}{\partial x} = m$, the slope of the string.
• The net vertical force can thus be rewritten: $T \Delta m$.
• By Newton's Second Law: $T \Delta m = (\mu \Delta x) \frac{\partial^{2}y}{\partial t^{2}} \hspace{0.1in}... ...e{0.1in} T \frac{\Delta m}{\Delta x} = \mu \frac{\partial^{2}y}{\partial t^{2}}$.
• As $\Delta x \rightarrow 0$,
  
  $$\lim_{\Delta x \rightarrow 0} \frac{\Delta m}{\Delta x} = \f... ...artial m}{\partial x} = \frac{\partial^{2} y}{\partial x^{2}}.$$
  
  

• The expression based on Newton's Second Law then becomes
  
  $$\frac{\partial^{2} y}{\partial t^{2}} = c^{2} \frac{\partial^{2} y}{\partial x^{2}},$$
  
  
  where $c = \sqrt{T/\mu}$ is the speed of wave motion on the string. This is the one-dimensional wave equation which describes small amplitude transverse waves on a stretched string.

Traveling Waves

• Solution to the wave equation of the form $y = f_{1}(ct - x) + f_{2}(ct + x)$.
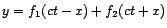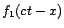• $f_{1}(ct - x)$ represents a wave traveling to the right with a velocity 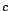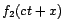$c$. $f_{2}(ct + x)$ represents a wave traveling to the left with the same velocity.
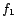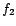• The functions $f_{1}$ and $f_{2}$ are arbitrary.

Wave Reflection

• At a fixed end, $y=0$. If the string is fixed at $x=0$, then $y=0$ and $f_{1}(ct) = -f_{2}(ct)$.
• At a free end, $\partial y/\partial x = 0$ because no transverse force is possible. In this case, $f_{1}(ct) = f_{2}(ct)$.

• In two or three dimensions, the angle an incident wavefront makes with a reflecting surface is equal to the angle of reflection.

Refraction

• A sudden or progressive change in wave speed will produce a change in propagation direction or a ``bending'' of the waves.

Diffraction

• Waves tend to bend around an obstacle.

• The amount of diffraction depends on the wavelength of the wave and on the size of the obstacle.

• If the wavelength is much larger than the object, the wave bends around it almost as if it isn't even there. When a wavelength is less than the size of an object, a ``shadow'' region will result.

The Doppler Effect

• Observer moving toward source:
  
  $$f' = f_{s} \frac{v + v_{o}}{v},$$
  
  
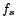  where $f_{s}$ is the frequency of the source, 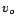$v_{o}$ is the speed of the observer, and 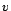$v$ is the speed of sound.

• Source moving toward observer:
  
  $$f = f_{s} \frac{v}{v-v_{s}},$$
  
  
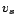  where $v_{s}$ is the speed of the source.

Sound Waves

• Longitudinal waves that travel in a solid, liquid, or gas.

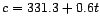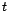• The speed of sound in air is approximately given by $c = 331.3 + 0.6 t$ where $t$ is the temperature of the air in degrees Celsius.