Sonification seminar - 10/9/03

Moving up in dimensional space, or, the world beyond pitch?

Topics:

  1. Beyond pitch mapping
  2. Pearl/Clark announce
  3. OSC in PD and MSP
  4. PD/DNA show and tell


An Introduction to timbre models

Wessel 2003


What timbre is (not)

tristimulus
spectral ballance

MDS (Grey, 1977)

Spectral centroid (brightness)
Spectral flux
Onset synchrony (bite)

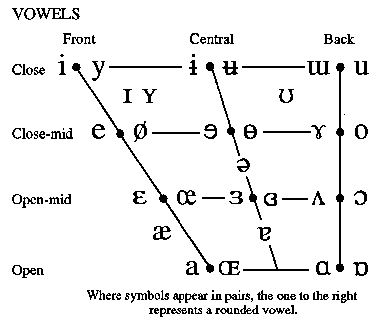
cardinal vowels

extreme positions: (close) High/Front  (open) Low/Back


general timbre analysis based on cardinal vowel space

IPA symbol Example
i beet, steal, eat, bee, chief
in, it, busy, limb, nearly(?)
eI able, bake, say
edge, elm, them, neck
at, ask, ham, sang
olive, onset, Tom, bomb
upper, uncle, but, rough
almost, ought, taut, caught, law, gnaw
oU oak, oval, boat, rose, no, sew
cook, stood, should, wolf
u ooze, oops, doom, whom, too, flu
First vowel of again, across
Second vowel of lemon, nation, sofa
aI ice, eyes, find, shine, by, sigh
aU out, hour, fowl, doubt, how, thou
I oil, oyster, coin, appoint, coy, boy
ju you, useful, pewter, jute, few, queue
earn, urge, turn, heard, fur, purr

why use vowels?  Sir Isaac Newton and beer




BUT:

In order to integrate new musical dimensions we must take into account perceptual issues such as:

Freq/Loudness relationship
Sensitivity and variation of percepts in (and between) ears
simple sine tone percept tests
and perceptual/cognitive issues involving arousal and attention
arousal - tendency to raise or lower physiological energy level)
    tonic (slow - sleep/wake, caffeine, alcohol)
    phasic (door slam)
    loudness, proximity, approch, surprise, opportunity, adress, emotive sounds
    low arousal - what is cute?

Habituation
stimulus-reaction- spontaneous recovery
300-3000 ms rule (300 - spontaneous recovery, 3000 - need to change - exclussive allocation)

attention - ability to comandeer perceptual awareness
active and passiv
passive - orienting response
rising pitch vs falling pitch (lullabies)

   

Critical Band

The range of frequencies that activate a single area of the basilar membrane. Measured perceptually by the smallest difference in which two sine tones are heard as distinct or as a single sine tone is masked by noise.

In human hearing, only those frequency components within a narrow band, called the critical band, will mask a given tone. Critical bandwidth varies with frequency but is usually between 1/6 and 1/3 octave.

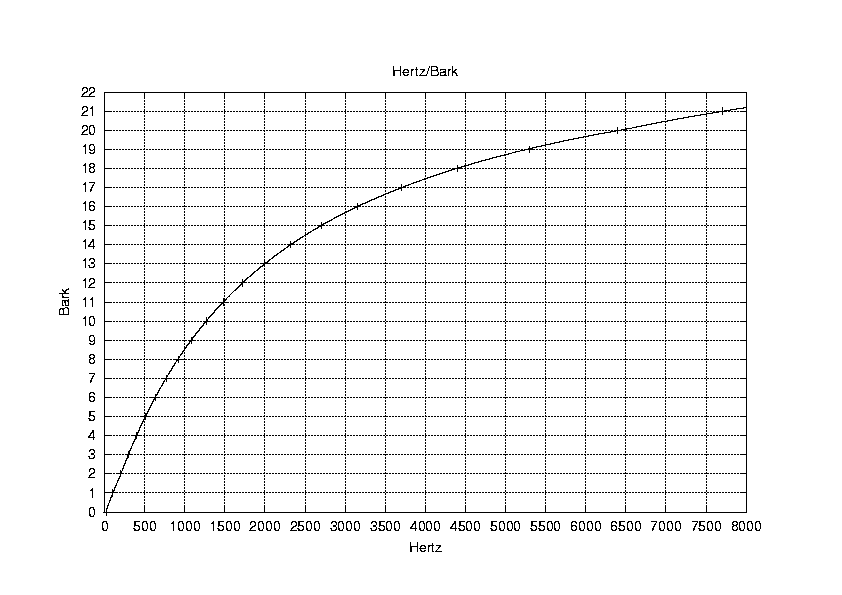
Bark Scale


The human auditory system consists of a series of bandpass filters (filters that have a certain center frequency and that increasingly attenuate signals as they deviate from that cf). The bandwidth of these auditory filters increases with higher frequencies and the precision of the frequency perception decreases.
Taking into account this property of the human auditory system, the Bark scale is a perceptually realistic scale of frequency.


The following conversion should be applied to transform frequency values (F) into Bark values:
Bark= [ (26.81*F) / (1960+F) ] - 0.53 where F= freq in Hz
(Traunmuller 1990)

other Bark Scale approximations include:

Zwicker & Terhardt
(1980)		 (1) Bark = 13tan-1(0.76f/1000) + 3.5tan-1(f/7500)2
(2) Bark = 8.7 + 14.2log10(f/1000)
Terhardt
(1979)		 (3) Bark = 13.3tan-1(0.75f/1000)
(4) Bark = 12.82tan-1(0.78f/1000) + 0.17(f/1000)1.4
Wang, Sekey & Gersho
(1992)		 (5) Bark = 6sinh-1(f/600)
Schroeder
(1977)		 (6) Bark = 7sinh-1(f/650)
Traunmüller
(1990)		 (7) Bark = 26.81/(1+(1960/f)) - 0.53


Frequencies and their bark equivalents, according to Traunmüller's approximation. The crosses on the plot correspond to the standard rounded bark scale.

plot of hertz and bark frequencies
(from Paul Carter)