- Writing recursive functions means writing functions that call themselves. Recursive functions solve problems in layers. An analogy can be done between recursion and the process of peeling an onion. Recursion is one of the most powerful ideas in computer science.
- A standard example of a recursive function is the factorial function. As you may recall , the factorial of a non negative integer is computed by taking the product of all the numbers from 1 up to the specified integer. It could be written as follows:
x! = factorial (x) = x * (x - 1) * (x - 2) * ... 1
- We can define this function recursively, that is, in terms of itself. Lets rewrite the definition of factorial in a recursive way:
factorial (x) = | 1 when x = 0
| x * (factorial (x - 1)) when x > 0
- This second definition of factorial can be directly converted into a recursive Lisp function:
(defun factorial (x)
"
computes the factorial of any integer number
"
(if (zerop x)
1
(* x (factorial (1- x)))))
- This function tests the value of x, if x equals zero then it returns 1; otherwise it returns the result of calling factorial on the value x minus 1. The 1- function, simply decrements its argument. The call (1- x) is equivalent to (- x 1).
(factorial 6)
-> 720
- The following flux diagram shows the way the factorial function works:
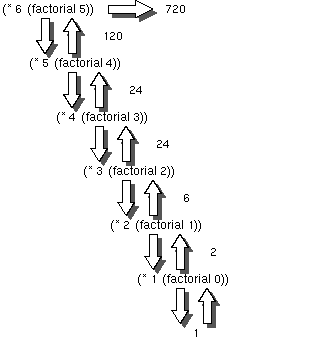
- In Lisp we can trace functions to see the way they are called in the flux of a program. If we trace factorial we get a diagram similar to the previous one:
(trace factorial)
-> (FACTORIAL)
(factorial 6)
1> (FACTORIAL 6)
2> (FACTORIAL 5)
3> (FACTORIAL 4)
4> (FACTORIAL 3)
5> (FACTORIAL 2)
6> (FACTORIAL 1)
7> (FACTORIAL 0)
<7 (FACTORIAL 1)
<6 (FACTORIAL 1)
<5 (FACTORIAL 2)
<4 (FACTORIAL 6)
<3 (FACTORIAL 24)
<2 (FACTORIAL 120)
<1 (FACTORIAL 720)
720
- We should untrace our function to avoid Lisp to continue printing its calls:
(untrace factorial)
- As factorial must compute all the factorials between 0 and the number passed as argument we can rewrite it as an intelligent function using an a-list:
;;; the empty association list
(defvar *factorial-a-list* '())
(defun factorial (x)
"
computes the factorial of any integer number
"
(if (assoc x *factorial-a-list*)
(cdr (assoc x *factorial-a-list*))
(let ((new (if (and (<= x 1)(plusp x))
1
(* x (factorial (1- x))))))
(push (cons x new) *factorial-a-list*)
new)))
- Calling factorial with 6 as argument has the side effect of teaching the function the factorials of 1 to 6:
(factorial 6)
-> 720
*factorial-a-list*
((6 . 720) (5 . 120) (4 . 24) (3 . 6) (2 . 2) (1 . 1))
- Other mathematic function simple to define recursively is fibonacci:
fibbobaci (x) = fibonacci (x - 2) + fibonacci (x - 1)
fibbobaci (x) = | 1 when x <= 2
| fibonacci (x - 2) + fibonacci (x - 1) when x > 2
- The simplest Lisp version of this function is:
(defun fibonacci (x)
"
computes the fibonacci number of x
"
(if (<= x 2)
1
(+ (fibonacci (- x 2))(fibonacci (1- x)))))
(loop for i from 1 to 7 do
(print (fibonacci i)))
- If we trace fibonacci we can see how many times we use it in one call to the function:
(trace fibonacci)
(fibonacci 7)
1> (fibonacci 7)
2> (fibonacci 5)
3> (fibonacci 3)
4> (fibonacci 1)
<4 (fibonacci 1)
4> (fibonacci 2)
<4 (fibonacci 1)
<3 (fibonacci 2)
3> (fibonacci 4)
4> (fibonacci 2)
<4 (fibonacci 1)
4> (fibonacci 3)
5> (fibonacci 1)
<5 (fibonacci 1)
5> (fibonacci 2)
<5 (fibonacci 1)
<4 (fibonacci 2)
<3 (fibonacci 3)
<2 (fibonacci 5)
2> (fibonacci 6)
3> (fibonacci 4)
4> (fibonacci 2)
<4 (fibonacci 1)
4> (fibonacci 3)
5> (fibonacci 1)
<5 (fibonacci 1)
5> (fibonacci 2)
<5 (fibonacci 1)
<4 (fibonacci 2)
<3 (fibonacci 3)
3> (fibonacci 5)
4> (fibonacci 3)
5> (fibonacci 1)
<5 (fibonacci 1)
5> (fibonacci 2)
<5 (fibonacci 1)
<4 (fibonacci 2)
4> (fibonacci 4)
5> (fibonacci 2)
<5 (fibonacci 1)
5> (fibonacci 3)
6> (fibonacci 1)
<6 (fibonacci 1)
6> (fibonacci 2)
<6 (fibonacci 1)
<5 (fibonacci 2)
<4 (fibonacci 3)
<3 (fibonacci 5)
<2 (fibonacci 8)
<1 (fibonacci 13)
13
(untrace fibonacci)
- This shows that it would be better to transform fibonacci into an intelligent function to, avoiding the computation of all the intermediate values:
;;; the empty association list
(defvar *fibonacci-a-list* '())
(defun fibonacci (x)
"
computes the fibonacci number of x
"
(if (assoc x *fibonacci-a-list*)
(cdr (assoc x *fibonacci-a-list*))
(let ((new (if (<= x 2)
1
(+ (fibonacci (- x 2))(fibonacci (1- x))))))
(push (cons x new) *fibonacci-a-list*)
new)))
- Calling fibonacci with 7 as argument has the side effect of teaching the function the fibonacci numbers of 1 to 7:
(fibonacci 7)
-> 13
*fibonacci-a-list*
((7 . 13) (6 . 8) (5 . 5) (4 . 3) (3 . 2) (2 . 1) (1 . 1))
- We can define recursive functions to operate over lists of notes. A very simple one can be a function that gives us the retrograde of a list of notes:
(defun retrograde (list-of-notes)
(if (null list-of-notes) nil ;;; 1
(append (last list-of-notes) ;;; 2
(retrograde (butlast list-of-notes))))) ;;; 3
- The function retrograde tests if the list-of-notes is empty (line 1), if it's not it appends (line 2) the last element of the list-of-notes in the front of the retrograde of the list-of-notes without its last element (butlast, line 3). When list-of-notes is empty retrograde returns an empty list (NIL, line 1) where it will append all the previous values coming from the other layers.
(retrograde '(a4 c5 b5))
-> (B5 C5 A4)
- We can trace retrograde to see how it works:
(trace retrograde)
(retrograde '(a4 c5 b5))
1> (RETROGRADE (A4 C5 B5))
2> (RETROGRADE (A4 C5))
3> (RETROGRADE (A4))
4> (RETROGRADE NIL)
<4 (RETROGRADE NIL)
<3 (RETROGRADE (A4))
<2 (RETROGRADE (C5 A4))
<1 (RETROGRADE (B5 C5 A4))
(B5 C5 A4)
(untrace retrograde)
- This particular program template can be used to create other functions. Lets create one function that take a list of notes and return the interval between the notes:
(defun intev-func (list-of-notes)
(if (null (rest list-of-notes)) NIL
(cons
(- (second list-of-notes)
(first list-of-notes))
(intev-func (rest list-of-notes)))))
;;; this macro calls the interv-func with MIDI note numbers
(defmacro intervals (list-of-notes)
`(intev-func (mapcar #'degree ,list-of-notes)))
- The call to intev-func is done indirectly by the macro intervals, that converts the notes from symbols to MIDI notes:
(intervals '(c3 g4 a7))
-> (19 38)
- Using this function we can define an inversion function:
(defun invert-func (intervs notes)
(if (null intervs) (nreverse notes)
(let ((new (- (first notes) (first intervs))))
(push new notes)
(invert-func (rest intervs) notes))))
(defmacro inversion (list-of-notes)
`(mapcar #'note (invert-func (intervals ,list-of-notes)
(list (degree (first ,list-of-notes))))))
- Again we are using an auxiliary macro to convert from and to note names. The inversion macro is our interface to the real inversion engine.
- We can trace invert-func to see how it works:
(trace invert-func)
(inversion '(c4 d4 e4))
1> (INVERT-FUNC (2 2) (60))
2> (INVERT-FUNC (2) (58 60))
3> (INVERT-FUNC NIL (56 58 60))
<3 (INVERT-FUNC (60 58 56))
<2 (INVERT-FUNC (60 58 56))
<1 (INVERT-FUNC (60 58 56))
(C4 AS3 GS3)
- These recursive functions can be combined with iterative functions:
(defun degree-l (l)
(mapcar #'degree l))
(defun note-l (l)
(mapcar #'note l))
(defun all-forms (raw)
(let*((orig (degree-l raw))
(inv (degree-l (inversion raw)))
(retro (degree-l (retrograde raw)))
(retro-inv (degree-l (inversion (retrograde raw))))
(o-list nil)
(i-list nil)
(r-list nil)
(ri-list nil))
(dotimes (i 12)
(push (mapcar #'(lambda (x) (+ x i)) orig) o-list)
(push (mapcar #'(lambda (x) (+ x i)) inv) i-list)
(push (mapcar #'(lambda (x) (+ x i)) retro) r-list)
(push (mapcar #'(lambda (x) (+ x i)) retro-inv) ri-list))
(list (mapcar #'note-l (nreverse o-list))
(mapcar #'note-l (nreverse i-list))
(mapcar #'note-l (nreverse r-list))
(mapcar #'note-l (nreverse ri-list)))))
- We can get all the forms of a given raw using the function all-forms. The output format is a list containing lists with all the transpositions in the order: (original inversion retrograde retrograde-inversion).
(all-forms '(c4 cs4 e4 ef4 d4 b4 fs4 g4 bf4 a4 af4 f4))
(((C4 CS4 E4 DS4 D4 B4 FS4 G4 AS4 A4 GS4 F4)
;;; original
(CS4 D4 F4 E4 DS4 C5 G4 GS4 B4 AS4 A4 FS4)
(D4 DS4 FS4 F4 E4 CS5 GS4 A4 C5 B4 AS4 G4)
(DS4 E4 G4 FS4 F4 D5 A4 AS4 CS5 C5 B4 GS4)
(E4 F4 GS4 G4 FS4 DS5 AS4 B4 D5 CS5 C5 A4)
(F4 FS4 A4 GS4 G4 E5 B4 C5 DS5 D5 CS5 AS4)
(FS4 G4 AS4 A4 GS4 F5 C5 CS5 E5 DS5 D5 B4)
(G4 GS4 B4 AS4 A4 FS5 CS5 D5 F5 E5 DS5 C5)
(GS4 A4 C5 B4 AS4 G5 D5 DS5 FS5 F5 E5 CS5)
(A4 AS4 CS5 C5 B4 GS5 DS5 E5 G5 FS5 F5 D5)
(AS4 B4 D5 CS5 C5 A5 E5 F5 GS5 G5 FS5 DS5)
(B4 C5 DS5 D5 CS5 AS5 F5 FS5 A5 GS5 G5 E5))
((C4 B3 GS3 A3 AS3 CS3 FS3 F3 D3 DS3 E3 G3)
;;; inversion
(CS4 C4 A3 AS3 B3 D3 G3 FS3 DS3 E3 F3 GS3)
(D4 CS4 AS3 B3 C4 DS3 GS3 G3 E3 F3 FS3 A3)
(DS4 D4 B3 C4 CS4 E3 A3 GS3 F3 FS3 G3 AS3)
(E4 DS4 C4 CS4 D4 F3 AS3 A3 FS3 G3 GS3 B3)
(F4 E4 CS4 D4 DS4 FS3 B3 AS3 G3 GS3 A3 C4)
(FS4 F4 D4 DS4 E4 G3 C4 B3 GS3 A3 AS3 CS4)
(G4 FS4 DS4 E4 F4 GS3 CS4 C4 A3 AS3 B3 D4)
(GS4 G4 E4 F4 FS4 A3 D4 CS4 AS3 B3 C4 DS4)
(A4 GS4 F4 FS4 G4 AS3 DS4 D4 B3 C4 CS4 E4)
(AS4 A4 FS4 G4 GS4 B3 E4 DS4 C4 CS4 D4 F4)
(B4 AS4 G4 GS4 A4 C4 F4 E4 CS4 D4 DS4 FS4))
((F4 GS4 A4 AS4 G4 FS4 B4 D4 DS4 E4 CS4 C4)
;;; retrograde
(FS4 A4 AS4 B4 GS4 G4 C5 DS4 E4 F4 D4 CS4)
(G4 AS4 B4 C5 A4 GS4 CS5 E4 F4 FS4 DS4 D4)
(GS4 B4 C5 CS5 AS4 A4 D5 F4 FS4 G4 E4 DS4)
(A4 C5 CS5 D5 B4 AS4 DS5 FS4 G4 GS4 F4 E4)
(AS4 CS5 D5 DS5 C5 B4 E5 G4 GS4 A4 FS4 F4)
(B4 D5 DS5 E5 CS5 C5 F5 GS4 A4 AS4 G4 FS4)
(C5 DS5 E5 F5 D5 CS5 FS5 A4 AS4 B4 GS4 G4)
(CS5 E5 F5 FS5 DS5 D5 G5 AS4 B4 C5 A4 GS4)
(D5 F5 FS5 G5 E5 DS5 GS5 B4 C5 CS5 AS4 A4)
(DS5 FS5 G5 GS5 F5 E5 A5 C5 CS5 D5 B4 AS4)
(E5 G5 GS5 A5 FS5 F5 AS5 CS5 D5 DS5 C5 B4))
((F4 D4 CS4 C4 DS4 E4 B3 GS4 G4 FS4 A4 AS4)
;;; retrograde-inversion
(FS4 DS4 D4 CS4 E4 F4 C4 A4 GS4 G4 AS4 B4)
(G4 E4 DS4 D4 F4 FS4 CS4 AS4 A4 GS4 B4 C5)
(GS4 F4 E4 DS4 FS4 G4 D4 B4 AS4 A4 C5 CS5)
(A4 FS4 F4 E4 G4 GS4 DS4 C5 B4 AS4 CS5 D5)
(AS4 G4 FS4 F4 GS4 A4 E4 CS5 C5 B4 D5 DS5)
(B4 GS4 G4 FS4 A4 AS4 F4 D5 CS5 C5 DS5 E5)
(C5 A4 GS4 G4 AS4 B4 FS4 DS5 D5 CS5 E5 F5)
(CS5 AS4 A4 GS4 B4 C5 G4 E5 DS5 D5 F5 FS5)
(D5 B4 AS4 A4 C5 CS5 GS4 F5 E5 DS5 FS5 G5)
(DS5 C5 B4 AS4 CS5 D5 A4 FS5 F5 E5 G5 GS5)
(E5 CS5 C5 B4 D5 DS5 AS4 G5 FS5 F5 GS5 A5)))
Back to LispWorkshop main page.
©1996-98 by Juan Pampin, juan@ccrma.stanford.edu
