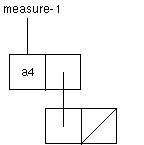
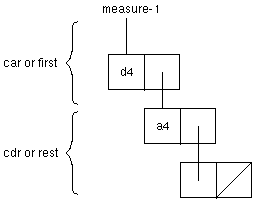
- Lets create the following list structure:
(defvar a-notes (list measure-1 measure-2 '(d4 c4)))
- The cell structure of a-notes is:

(car a-notes) ;;; this is measure-1
(car (cdr a-notes)) ;;; this is measure-2
(car (cdr (cdr a-notes))) ;;; the same as measure-1
- The second element of both measure-1 and measure-2 are the same:
(second (car a-notes)) or (second (first a-notes)) or (nth 1 (first a-notes))
(second (cadr a-notes)) or (second (first (rest a-notes))) or (nth 1 (nth 0 (rest a-notes)))
and the first and last elements of a-notes have the same content:
(first a-notes)
(second (rest a-notes))
- The predicate eq can be used to compare Lisp forms:
(eq (nth 1 (first a-notes)) (nth 1 (nth 0 (rest a-notes))))
(eq (first a-notes) (second (rest a-notes)))
- In the first case eq answers T, because this two objects are exactly the same: the symbol C4 is identical to itself. But in the second case eq answers NIL because the two list are stored in different memory allocations. Lisp has different predicates to compare forms at different levels. The predicate eq is the highest in the hierarchy of predicates, it can get you into trouble if you are dealing with anything but symbols:
(eq 1.0 1.0)
(eq "hello" "hello")
- The following in the hierarchy is the predicate eql
(eql 1.0 1.0)
(eql (nth 1 (first a-notes)) (nth 1 (nth 0 (rest a-notes))))
but:
(eql (first a-notes) (second (rest a-notes)))
(eql "hello" "hello")
- Eql is less restrictive that eq but it still considers the two lists with the same contents to be different. One step further is the predicate equal:
(equal (first a-notes) (second (rest a-notes)))
(equal "hello" "hello")
but:
(equal 1 1.0)
- The function equal treats two objects as equivalent if they are symbols and they are eq, if they are numeric constants and are eql, or if they are two objects of the same type and print the same way.
- The less restrictive of all the equivalence predicates is equalp
(equalp 1 1.0)
(equalp "Hello" "HELLO")
- Equalp returns T if its arguments are equal, or if its arguments are numbers that can be coerced to the same type and have the same value.
- The hierarchy of the equivalence predicates is:
eq
eql
equal
equalp