5.1 Anti-aliasing

The Nyquist criterion dictates that all signals must be bandlimited to less than half the sampling rate of the sampling system. Many signals already have a limited spectrum, so this is not a problem. However, for broad spectrum signals, an analog lowpass filter must be placed before the data acquisition system. The minimum attenuation of this filter at the aliasing frequency should be at least: 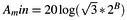where B is the number of bits of the ADC. This formula is derived from the fact that there is a minimum noise level inherent in the sampling process and there is no need to attenuate the sensor signal more than to below this noise level.

5.1.1 Problems with the Anti-aliasing Filter:

1. Time Response: In designing an anti-aliasing filter, there is a temptation to have it's attenuation roll-off extremely quickly. The way to achieve this is to increase the order of the filter (see the previous discussion of filter order). A so-called brick-wall filter (one with infinitely high order), however, causes a sinc function time response that decays proportionally to 1/t. What this means is that an extremely high order filter that eliminates all signals above the cutoff frequency will cause signals that change rapidly to ring on for a long time. A very undesirable effect.
2. Phase Distortion / Time delay: Most analog filters have a non-linear phase response. This a problem since non-linear phase causes an unequal time (group) delay as a function of frequency. The higher frequency signals will arrive later than low frequency signals. This can especially be a problem when multiple sensor outputs are compared such as when using a microphone array.
3. Amplitude Distortion: By definition, the filter will modify the frequency structure of the sensor signal which is usually not desired

5.1.2 Solutions:

1. Increase the sampling rate of the ADC. This allows the antialiasing filter to have a higher cutoff frequency and still eliminate aliasing. This enables the following:
   1. The filter rolloff can be more shallow - allowing a better time response
   2. The frequency response of the filter does not attenuate the lower sensor frequencies of interest
   3. Phase distortion is strongest around the cutoff frequency of the filter so if this is pushed higher, it will not affect the sensor frequencies this cutoff
2. Have linear phase filters. This, of course, will reduce the phase distortion problems.