A general characteristic of musically useful horns is that their internal bore profile is well approximated with a Bessel horn [2]. Although any real instrument bell will show significant deviations from this approximation in its bore shape and acoustic reflectance, a theoretically derived Bessel horn reflection function may serve as a suitable generalized target-response for developing effective digital filter design techniques. In order to obtain such a target-response, the pressure reflectance of a Bessel horn that approximates the shape of a trumpet bell was computed as in [9].
As shown in Fig. 2, the Bessel horn
reflection impulse response has a slow, quasi-exponentionally growing
portion at the beginning, corresponding to the smoothly increasing taper
angle of the horn. A one-pole TIIR filter gives a
truncated exponential impulse response
![]() , for
, for
![]() , and zero afterwards. We can use this truncated
exponential to efficiently implement the initial growing trend in the horn
response (
, and zero afterwards. We can use this truncated
exponential to efficiently implement the initial growing trend in the horn
response (![]() ). We found empirically that improved accuracy is
obtained by using the sum of an exponential and a constant, i.e.,
). We found empirically that improved accuracy is
obtained by using the sum of an exponential and a constant, i.e.,
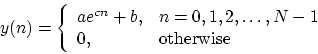
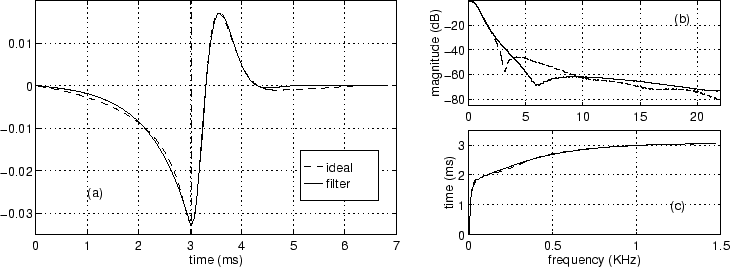
In Fig. 2, the TIIR horn filter structure (using a 3rd-order IIR tail filter approximation) is compared with the theoretical response. The phase delay (directly proportional to the ``effective length'' of the bell for standing waves), has a particularly good fit, which is important for accurate musical resonance frequencies of a brass instrument.
|