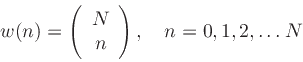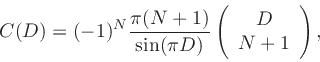Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Lagrange interpolation is a well known, classical technique for
interpolation [#!Hildebrand!#]. It is also called Waring-Lagrange
interpolation, since Waring actually published it 16 years before
Lagrange [#!Meijering02!#, p. 323]. Given a set of n+1 known
samples f(xk),
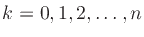 , the problem is to find the
unique order n polynomial y(x) which interpolates the samples.
The solution can be expressed as a linear combination of elementary
nth order polynomials:
, the problem is to find the
unique order n polynomial y(x) which interpolates the samples.
The solution can be expressed as a linear combination of elementary
nth order polynomials:
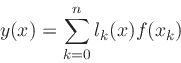 |
(17) |
where
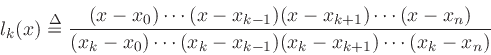 |
(18) |
From the numerator of the above definition, we see that lk(x) is an
order n polynomial having zeros at all of the samples except the kth.
The denominator is simply the constant which normalizes its value to 1 at
xk. Thus, we have
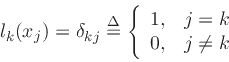 |
(19) |
In other words, the polynomial lk is the kth basis polynomial for constructing a polynomial interpolation of order n over the n+1
sample points xk.
In the case of an infinite number of equally spaced samples, with spacing
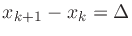 , the Lagrangian basis
polynomials converge to shifts of the sinc function, i.e.,
, the Lagrangian basis
polynomials converge to shifts of the sinc function, i.e.,
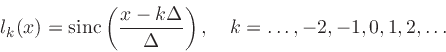 |
(20) |
where
A simple argument is based on the fact that any analytic function is
determined by its zeros and its value at one point. Since
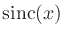 is zero on all the integers except 0, and since
is zero on all the integers except 0, and since
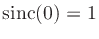 , it
must coincide with the infinite-order Lagrangian basis polynomial for
the sample at x=0 which also has its zeros on the nonzero integers
and equals 1 at x=0.
, it
must coincide with the infinite-order Lagrangian basis polynomial for
the sample at x=0 which also has its zeros on the nonzero integers
and equals 1 at x=0.
The equivalence of sinc interpolation to Lagrange interpolation was
apparently first published by the mathematician Borel in 1899, and has
been rediscovered many times since [#!Meijering02!#, p. 325].
A direct proof can be based on the equivalance between Lagrange
interpolation and windowed-sinc interpolation using a ``scaled
binomial window'' [#!KootsookosAndWilliamson95!#,#!VesaT!#]. That is,
for a fractional sample delay of D samples, multiply the
shifted-by-D, sampled, sinc function
by a binomial window
and normalize by [#!VesaT!#]
which scales the interpolating filter to have a unit L2 norm, to
obtain the Nth-order Lagrange interpolating filter
Since the binomial window converges to the Gaussian window as 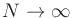 ,
and since the window gets wider and wider, approaching a unit constant in
the limit, the convergence of Lagrange to sinc interpolation can be seen.
,
and since the window gets wider and wider, approaching a unit constant in
the limit, the convergence of Lagrange to sinc interpolation can be seen.
A more recent alternate proof appears in [#!Yekta09!#].
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download resample.pdf
[How to cite and copy this work] [Comment on this page via email]
![]() , the problem is to find the
unique order n polynomial y(x) which interpolates the samples.
The solution can be expressed as a linear combination of elementary
nth order polynomials:
, the problem is to find the
unique order n polynomial y(x) which interpolates the samples.
The solution can be expressed as a linear combination of elementary
nth order polynomials:
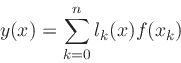
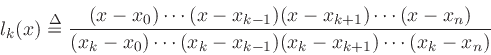
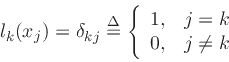
![]() , the Lagrangian basis
polynomials converge to shifts of the sinc function, i.e.,
, the Lagrangian basis
polynomials converge to shifts of the sinc function, i.e.,
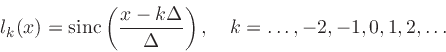
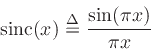
![\begin{displaymath}
h_s(n) = \mbox{sinc}(n-D) = \frac{\sin[\pi(n-D)]}{\pi(n-D)}
\end{displaymath}](img132.png)