Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
If the window 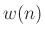 has the Constant OverLap-Add (COLA)
property at hop-size
has the Constant OverLap-Add (COLA)
property at hop-size 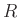 :
:
then the individual DTFTs will sum to the DTFT of all 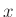 :
:
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
[Comment on this page via email]
![]() has the Constant OverLap-Add (COLA)
property at hop-size
has the Constant OverLap-Add (COLA)
property at hop-size ![]() :
:
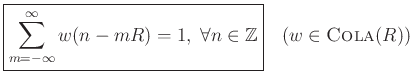
![\begin{eqnarray*}
\sum_{m=-\infty}^\infty X_m(\omega)
&\mathrel{\stackrel{\mathrm{\Delta}}{=}}&
\sum_{m=-\infty}^\infty\sum_{n=-\infty}^{\infty} x(n) w(n-mR) e^{-j\omega n}\\
&=& \sum_{n=-\infty}^{\infty} x(n) e^{-j\omega n}
\underbrace{\sum_{m=-\infty}^\infty w(n-mR)}_{1\hbox{ if }w\in\hbox{\sc Cola}(R)}
\\
&=& \sum_{n=-\infty}^{\infty} x(n) e^{-j\omega n} \\
&\mathrel{\stackrel{\mathrm{\Delta}}{=}}& \hbox{\sc DTFT}_\omega(x) = X(\omega)\\ [20pt]
\longleftrightarrow \quad x(n) %= \IDTFT_n(X)
&=& \frac{1}{2\pi}\int_{-\pi}^{\pi} X(\omega) e^{j\omega n}d\omega
\end{eqnarray*}](img7.png)