Identifying Chirp Rate

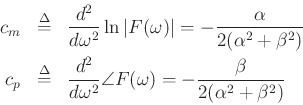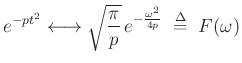
Above we showed

$$e^{-pt^2} \longleftrightarrow \sqrt{\frac{\pi}{p}} \, e^{-\frac{\omega^2}{4p}}\;\isdef \;F(\omega)$$

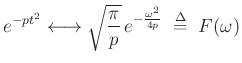
Setting $p=\alpha - j\beta$ gives

$$e^{-\alpha t^2} e^{j\beta t^2} \longleftrightarrow \sqrt{\frac{\pi}{\alpha-j\beta}} \, e^{-\frac{\alpha}{4(\alpha^2+\beta^2)}\omega^2} e^{-j\frac{\beta}{4(\alpha^2+\beta^2)}\omega^2}$$

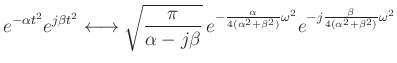
The log magnitude Fourier transform is given by

$$\ln\left\vert F(\omega)\right\vert = \hbox{constant} -\frac{\alpha}{4(\alpha^2+\beta^2)}\omega^2$$

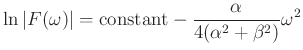
and the phase is

$$\angle F(\omega) = \hbox{constant} -\frac{\beta}{4(\alpha^2+\beta^2)}\omega^2$$

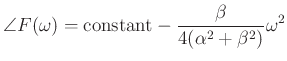
Note that both log-magnitude and (unwrapped) phase are parabolas in $\omega$ .

In practice, it is simple to estimate the curvature at a spectral peak using parabolic interpolation:

$$\begin{eqnarray*} c_m &\isdef & \frac{d^2}{d\omega^2} \ln\vert F(\omega)\vert = - \frac{\alpha}{2(\alpha^2+\beta^2)}\\ c_p &\isdef & \frac{d^2}{d\omega^2} \angle F(\omega) = - \frac{\beta}{2(\alpha^2+\beta^2)} \end{eqnarray*}$$